The summary of the process is:
-
Use NREL PV Watts modeling to obtain hourly power estimates.
-
Compare the hourly estimates to seasonal PJM demand data.
-
Obtain historical, hourly pricing data for PJM.
-
Determine how much demand not being met by panels is cost-effective to be arbitraged by batteries with the extra DC production
There are many assumptions and simplifications. I'd be happy if this had one sig fig accuracy. The one that bothers me the most is that when you create an average day and match it to peak demand, the average includes some days that might produce more than demand. In real life, electricity demand constrains output. Batteries and higher DC to AC ratios make this less relevant. So the cases with no storage and especially the lowest DC to AC ratios are probably overstated.
PV Watts
NREL PV Watts Calculator
These are the settings I put in the PV Watts model. Charlottesville is a random location within PJM. I titled the array slightly more than max power production so that the ratio of summer to winter power production would be more favorable. The calculator offers an option to download the hourly data as a CSV file.
Requested Location: Charlottesville, VA
Location: Lat, Lon: 38.05, -78.46
Lat (deg N): 38.05
Long (deg W): 78.46
Elev (m): 134.16000366211
DC System Size (kW): 1
Module Type: Standard
Array Type: 1-Axis Tracking
Array Tilt (deg): 45
Array Azimuth (deg): 180
System Losses: 14.08
Invert Efficiency: 96
DC to AC Size Ratio: 1.0
Ground Coverage Ratio: 0.3
PJM Comparison
I'll walk through the code step by step then put the entire script at the bottom.
First, we import the PV Watts CSV data:
import csv
pv_csv = open('/path/to/file/pvwatts_hourly-dcac1.csv')
pv_reader = csv.reader(pv_csv)
pv_data = list(pv_reader)
I interpolated the PJM data from this chart:
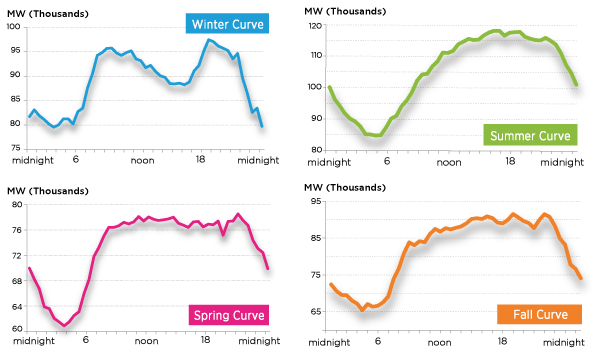
Source: PJM Learning Center
pjm_data = [[82,83,81,79,81,80,85,90,95,95,93,92,92,91,89,88,88,91,92,96,95,90,
85,80],[70,68,64,61,62,66,68,72,76,77,78,77,77,76,76,76,77,76,77,78,77,76,72,69],[100,
95,90,85,85,87,90,95,100,105,110,112,114,115,116,117,118,117,116,115,115,110,105,100],[73,
71,70,68,65,66,67,73,79,82,85,87,87,88,89,90,91,89,91,88,91,85,80,75]]
The structure is [[winter hours 0-23], [spring hours 0-23], [summer hours 0-23], [fall hours 0-23]] with the index in the nested arrays being the hour.
And the sum of the average day for each season, using Riemann Sums:
pjm_daily_total_by_season = [2113, 1746, 2512, 1930]
We need a data structure that allows the grouping of all data points for an hour and season. This function generates a data structure similar to our PJM data.
def hourly_data_structure():
return [[[] for _ in range(24)], [[] for _ in range(24)], [[] for _ in range(24)], [[] for _ in range(24)]]
And we need a data structure for averaged values, the same as the PJM daily total data structure.
def seasonal_data_structure():
return [[],[],[],[]]
We have to sort and average all the hourly data to create an "average day" to match our PJM average days for each season.
#split data up by season
seasons = [0,0,0,0]
seasons[0] = [hour for hour in pv_data[19:-1] if hour[0] in ['12','1','2']]
seasons[1] = [hour for hour in pv_data[19:-1] if hour[0] in ['3','4','5']]
seasons[2] = [hour for hour in pv_data[19:-1] if hour[0] in ['6','7','8']]
seasons[3] = [hour for hour in pv_data[19:-1] if hour[0] in ['9','10','11']]
#Put data in the correct hour
hourly_pv_data = hourly_data_structure()
for i,season in enumerate(seasons):
for hour in season:
#index 2 of hour is the hour of the day in the PV Watts data
hourly_pv_data[i][int(hour[2])].append(hour)
The way the PV Watts outputs the data makes it challenging to compare DC to AC ratios the way I wanted to. We will use one case and manually size the system using ratios and calculate our own AC outputs from DC values.
#size the inverter based on max output
max_dc = max([float(hour[9]) for hour in pv_data[19:-1]])
inverter_efficiency = 0.96
inverter_size = max_dc*inverter_efficiency
#set ratio and battery size
dc_ac_ratio = 2
battery_size_gwh = 848
Now, let's average all our data points to create an average day for each season.
#average each hour
hourly_ac_averages = seasonal_data_structure()
hourly_dc_averages = seasonal_data_structure()
for i,season in enumerate(hourly_pv_data):
for hours in season:
#The DC and AC data are index 9,10
dc_data = [float(hour[9])*dc_ac_ratio for hour in hours]
ac_data = [dc_hour * inverter_efficiency if dc_hour * inverter_efficiency < inverter_size else inverter_size for dc_hour in dc_data]
ac_average = (sum(ac_data)/len(ac_data))
dc_average = (sum(dc_data)/len(dc_data))
hourly_ac_averages[i].append(ac_average)
hourly_dc_averages[i].append(dc_average)
Our averages are for a 1 kW AC system. The system size is adjusted to meet 100% of the noon summer demand, using the 1:1 DC to AC ratio. The tilt we set for our panels means peak production doesn't always happen in summer, and the inverter is not 100% utilized. Increasing DC to AC ratio uses more of the inverter and decreases our adjusted system size, which is not the comparison I wanted.
#identify noon, summer demand to size capacity
summer_noon_demand = pjm_data[2][11]
#Size using 1:1 ratio
summer_noon_pv_average = hourly_dc_averages[2][11]*inverter_efficiency/dc_ac_ratio
# convert watts to thousands of MW, please forgive the unit conversion sins
capacity_adjustment = summer_noon_demand/summer_noon_pv_average
# loop through to make adjustment
for i,season in enumerate(hourly_ac_averages):
for j,hourly_average in enumerate(season):
hourly_ac_averages[i][j] = hourly_average * capacity_adjustment
hourly_dc_averages[i][j] = hourly_dc_averages[i][j] * capacity_adjustment
#if solar output is greater than demand, AC output is curtailed
if hourly_ac_averages[i][j] > pjm_data[i][j]:
hourly_ac_averages[i][j] = pjm_data[i][j]
We can get the total energy usage for each day and see what solar contributed.
# total electricity usage in GWh for a typical day in each season
sum_daily_ac_average_by_season = [sum(season) for season in hourly_ac_averages]
print('market share, no storage: ',sum(sum_daily_ac_average_by_season)/sum(pjm_daily_total_by_season))
Battery Arbitrage
Now to add some batteries. We have extra DC power. But the batteries have to be profitable. We can download a historical section of electricity price data from PJM's website. PJM Data Miner. I used June 2020-June 2021. I was a little worried about pandemic effects, but I spot-checked the 2019 data, and the basic averages were pretty close.
#import csv
price_csv = open('/path/to/file/rt_da_monthly_lmps.csv')
price_reader = csv.reader(price_csv)
price_data = list(price_reader)
price_seasons = [0,0,0,0]
hourly_price_data = hourly_data_structure()
And sort the data by season:
price_seasons = [0,0,0,0]
price_seasons[0] = [hour for hour in price_data[1:] if hour[1][0:2] in ['12','1/','2/']]
price_seasons[1] = [hour for hour in price_data[1:] if hour[1][0:2] in ['3/','4/','5/']]
price_seasons[2] = [hour for hour in price_data[1:] if hour[1][0:2] in ['6/','7/','8/']]
price_seasons[3] = [hour for hour in price_data[1:] if hour[1][0:2] in ['9/','10','11']]
Then sort by the hour. The PJM data is not as friendly to our data structure, so there is a dictionary to put the data in the correct hour.
hourly_price_data = hourly_data_structure()
hour_dictionary = {'12:00:00 AM':0,' 1:00:00 AM':1,' 2:00:00 AM':2,' 3:00:00 AM':3,
' 4:00:00 AM':4,' 5:00:00 AM':5,' 6:00:00 AM':6,' 7:00:00 AM':7,' 8:00:00 AM':8,
' 9:00:00 AM':9,'10:00:00 AM':10,'11:00:00 AM':11,'12:00:00 PM':12,' 1:00:00 PM':13,
' 2:00:00 PM':14,' 3:00:00 PM':15,' 4:00:00 PM':16,' 5:00:00 PM':17,' 6:00:00 PM':18,
' 7:00:00 PM':19,' 8:00:00 PM':20,' 9:00:00 PM':21,'10:00:00 PM':22,'11:00:00 PM':23}
for i,season in enumerate(price_seasons):
for hour in season:
hourly_price_data[i][hour_dictionary[hour[1][-11:]]].append(hour)
Now we can create our hourly price averages for an average day in each season:
hourly_price_averages = seasonal_data_structure()
for p,season in enumerate(hourly_price_data):
for hours in season:
price_point = [float(hour[8]) for hour in hours]
price_average = (sum(price_point)/len(price_point))
hourly_price_averages[p].append(price_average)
Ok, now we have solar data and price data. We will have to determine how much energy is available to arbitrage, how much demand there is, and specify our battery capacity. Here are a few things I might be glossing over:
-
High battery capacity to power requirements for 10+ hour storage means power was not considered a limitation.
-
This doesn't account for all the things batteries can do to earn money, including frequency regulation or multiple cycles per day. We are assuming a 24-hour cycle.
-
I left out battery efficiency. Depending on the solar farm and battery DC voltage, the efficiency will be 94%-97%.
We set up data structures for demand, extra DC electricity, and arbitrage prices.
sum_daily_battery_contribution = []
hourly_extra_demand = hourly_data_structure()
hourly_extra_dc_power = hourly_data_structure()
arb_data = seasonal_data_structure()
Run through each hour to determine extra demand, what prices are, and what extra DC is available.
for l,season in enumerate(hourly_ac_averages):
for m,hour in enumerate(season):
extra_demand = pjm_data[l][m] - hourly_ac_averages[l][m]
#there is no power to arbitrage if solar satisfies it
if extra_demand > 0:
#save hourly price and demand so we can calculate battery revenue
arb_data[l].append([hourly_price_averages[l][m],extra_demand])
#we need what dc power is extra to charge batteries
extra_dc_power = hourly_dc_averages[l][m] - hourly_ac_averages[l][m]
hourly_extra_demand[l][m] = extra_demand
hourly_extra_dc_power[l][m] = extra_dc_power
Now we have to sum our hours to get our daily demand:
for q,season in enumerate(hourly_extra_demand):
#determine which factor limits arbitrage between demand, extra dc supply, or battery capacity
battery_contribution = min(sum(season), sum(hourly_extra_dc_power[q]), battery_size_gwh)
sum_daily_battery_contribution.append(battery_contribution)
Next, we need to approximate battery revenue per cycle. Batteries will arb the highest prices first, so we order the juiciest hours first.
#sort price-demand blocks from highest price to lowest price
for i,season_day in enumerate(arb_data):
arb_data[i] = sorted(season_day, key = lambda x: x[0], reverse=True)
And now we use a weighted average to see what the average price our batteries got was.
arb_weights = 0
for i, season_day in enumerate(arb_data):
battery_available = sum_daily_battery_contribution[i]
demand_met = 0
j = 0
#keep going through hours until battery is empty or demand is met
while demand_met < battery_available and j < 24:
demand_met = demand_met + arb_data[i][j][1]
arb_weights = arb_weights + arb_data[i][j][1]*arb_data[i][j][0]
j += 1
arb_price = arb_weights/sum(sum_daily_battery_contribution)
Now that we know revenue, we can guess the battery CAPEX needed to break even.
#battery cost assumptions
cycles_to_80_percent = 5000
fixed_opex_kwh = 0.005
discount_factor = 1.3
capacity_payment_kwh = 0.015 #assume 10 hour system
utilization = sum(sum_daily_battery_contribution)/(battery_size_gwh*4)
battery_breakeven_capex = round(cycles_to_80_percent * (arb_price/1000 - fixed_opex_kwh) / discount_factor * utilization)
battery_breakeven_capex_capacity_payment = round(cycles_to_80_percent * (arb_price/1000 - fixed_opex_kwh + capacity_payment_kwh) / discount_factor * utilization)
And we can do our final calculations:
print('arb price: ',arb_price, ' $/MWh')
print('battery_breakeven_capex: ',battery_breakeven_capex, ' $/kWh')
print('battery_breakeven_capex capacity payment: ',battery_breakeven_capex_capacity_payment, ' $/kWh')
print('battery contribution: ',sum_daily_battery_contribution, 'GWh')
print('marketshare, storage: ',round((sum(sum_daily_ac_average_by_season)+sum(sum_daily_battery_contribution))/sum(pjm_daily_total_by_season),2))
Full code:
import csv
#python3 desktop/scripts/hourlysolarcalcs.py
#import csv
pv_csv = open('/users/austinvernon/downloads/pvwatts_hourly-dcac1.csv')
pv_reader = csv.reader(pv_csv)
pv_data = list(pv_reader)
pjm_data = [[82,83,81,79,81,80,85,90,95,95,93,92,92,91,89,88,88,91,92,96,95,90,
85,80],[70,68,64,61,62,66,68,72,76,77,78,77,77,76,76,76,77,76,77,78,77,76,72,69],[100,
95,90,85,85,87,90,95,100,105,110,112,114,115,116,117,118,117,116,115,115,110,105,100],[73,
71,70,68,65,66,67,73,79,82,85,87,87,88,89,90,91,89,91,88,91,85,80,75]]
pjm_daily_total_by_season = [2113, 1746, 2512, 1930]
def hourly_data_structure():
return [[[] for _ in range(24)], [[] for _ in range(24)], [[] for _ in range(24)], [[] for _ in range(24)]]
def seasonal_data_structure():
return [[],[],[],[]]
#split data up by season
seasons = [0,0,0,0]
seasons[0] = [hour for hour in pv_data[19:-1] if hour[0] in ['12','1','2']]
seasons[1] = [hour for hour in pv_data[19:-1] if hour[0] in ['3','4','5']]
seasons[2] = [hour for hour in pv_data[19:-1] if hour[0] in ['6','7','8']]
seasons[3] = [hour for hour in pv_data[19:-1] if hour[0] in ['9','10','11']]
#sort hour data to prepare for averages by hour
hourly_pv_data = hourly_data_structure()
for i,season in enumerate(seasons):
for hour in season:
#index 2 of hour is the hour of the day for solar
hourly_pv_data[i][int(hour[2])].append(hour)
max_dc = max([float(hour[9]) for hour in pv_data[19:-1]])
inverter_efficiency = 0.96
inverter_size = max_dc*inverter_efficiency
dc_ac_ratio = 2
battery_size_gwh = 848
#average each hour
hourly_ac_averages = seasonal_data_structure()
hourly_dc_averages = seasonal_data_structure()
for i,season in enumerate(hourly_pv_data):
for hours in season:
#The DC and AC data are index 9,10
dc_data = [float(hour[9])*dc_ac_ratio for hour in hours]
ac_data = [dc_hour*inverter_efficiency if dc_hour*inverter_efficiency < inverter_size else inverter_size for dc_hour in dc_data]
ac_average = (sum(ac_data)/len(ac_data))
dc_average = (sum(dc_data)/len(dc_data))
hourly_ac_averages[i].append(ac_average)
hourly_dc_averages[i].append(dc_average)
#identify noon, summer demand to size capacity
summer_noon_demand = pjm_data[2][11]
#Use the 1 ratio plant to size.
summer_noon_pv_average = hourly_dc_averages[2][11]*inverter_efficiency/dc_ac_ratio
# convert watts to thousands of MW, please forgive the unit conversion sins
capacity_adjustment = summer_noon_demand/summer_noon_pv_average
# loop through to make adjustment
for i,season in enumerate(hourly_ac_averages):
for j,hourly_average in enumerate(season):
hourly_ac_averages[i][j] = hourly_average * capacity_adjustment
hourly_dc_averages[i][j] = hourly_dc_averages[i][j] * capacity_adjustment
#if solar output is greater than demand, AC output is curtailed
if hourly_ac_averages[i][j] > pjm_data[i][j]:
hourly_ac_averages[i][j] = pjm_data[i][j]
# total electricity usage in GWh for a typical day in each season
sum_daily_ac_average_by_season = [sum(season) for season in hourly_ac_averages]
print('market share, no storage: ',round(sum(sum_daily_ac_average_by_season)/sum(pjm_daily_total_by_season),2))
#import csv
price_csv = open('/users/austinvernon/downloads/rt_da_monthly_lmps.csv')
price_reader = csv.reader(price_csv)
price_data = list(price_reader)
price_seasons = [0,0,0,0]
price_seasons[0] = [hour for hour in price_data[1:] if hour[1][0:2] in ['12','1/','2/']]
price_seasons[1] = [hour for hour in price_data[1:] if hour[1][0:2] in ['3/','4/','5/']]
price_seasons[2] = [hour for hour in price_data[1:] if hour[1][0:2] in ['6/','7/','8/']]
price_seasons[3] = [hour for hour in price_data[1:] if hour[1][0:2] in ['9/','10','11']]
hourly_price_data = hourly_data_structure()
hour_dictionary = {'12:00:00 AM':0,' 1:00:00 AM':1,' 2:00:00 AM':2,' 3:00:00 AM':3,
' 4:00:00 AM':4,' 5:00:00 AM':5,' 6:00:00 AM':6,' 7:00:00 AM':7,' 8:00:00 AM':8,
' 9:00:00 AM':9,'10:00:00 AM':10,'11:00:00 AM':11,'12:00:00 PM':12,' 1:00:00 PM':13,
' 2:00:00 PM':14,' 3:00:00 PM':15,' 4:00:00 PM':16,' 5:00:00 PM':17,' 6:00:00 PM':18,
' 7:00:00 PM':19,' 8:00:00 PM':20,' 9:00:00 PM':21,'10:00:00 PM':22,'11:00:00 PM':23}
for i,season in enumerate(price_seasons):
for hour in season:
hourly_price_data[i][hour_dictionary[hour[1][-11:]]].append(hour)
hourly_price_averages = seasonal_data_structure()
for p,season in enumerate(hourly_price_data):
for hours in season:
price_point = [float(hour[8]) for hour in hours]
price_average = (sum(price_point)/len(price_point))
hourly_price_averages[p].append(price_average)
#usage that is above clearing price
#check each AC average to see if it exceeds demand. If it does, set figure to match demand
sum_daily_battery_contribution = []
hourly_extra_demand = hourly_data_structure()
hourly_extra_dc_power = hourly_data_structure()
arb_data = seasonal_data_structure()
for l,season in enumerate(hourly_ac_averages):
for m,hour in enumerate(season):
extra_demand = pjm_data[l][m] - hourly_ac_averages[l][m]
if extra_demand > 0:
arb_data[l].append([hourly_price_averages[l][m],extra_demand])
extra_dc_power = hourly_dc_averages[l][m] - hourly_ac_averages[l][m]
hourly_extra_demand[l][m] = extra_demand
hourly_extra_dc_power[l][m] = extra_dc_power
#sum daily, sum PJM to get market share
for q,season in enumerate(hourly_extra_demand):
battery_contribution = min(sum(season), sum(hourly_extra_dc_power[q]), battery_size_gwh)
sum_daily_battery_contribution.append(battery_contribution)
#sort price-demand blocks from highest price to lowest price
for i,season_day in enumerate(arb_data):
arb_data[i] = sorted(season_day, key = lambda x: x[0], reverse=True)
arb_weights = 0
for i, season_day in enumerate(arb_data):
battery_available = sum_daily_battery_contribution[i]
demand_met = 0
j = 0
while demand_met < battery_available and j < 24:
demand_met = demand_met + arb_data[i][j][1]
arb_weights = arb_weights + arb_data[i][j][1]*arb_data[i][j][0]
j += 1
arb_price = arb_weights/sum(sum_daily_battery_contribution)
#battery cost assumptions
cycles_to_80_percent = 5000
fixed_opex_kwh = 0.005
discount_factor = 1.3
capacity_payment_kwh = 0.015 #assume 10 hour system
utilization = sum(sum_daily_battery_contribution)/(battery_size_gwh*4)
battery_breakeven_capex = round(cycles_to_80_percent * (arb_price/1000 - fixed_opex_kwh) / discount_factor * utilization)
battery_breakeven_capex_capacity_payment = round(cycles_to_80_percent * (arb_price/1000 - fixed_opex_kwh + capacity_payment_kwh) / discount_factor * utilization)
print('arb price: ',arb_price, ' $/MWh')
print('battery_breakeven_capex: ',battery_breakeven_capex, ' $/kWh')
print('battery_breakeven_capex capacity payment: ',battery_breakeven_capex_capacity_payment, ' $/kWh')
print('battery contribution: ',sum_daily_battery_contribution, 'GWh')
print('marketshare, storage: ',round((sum(sum_daily_ac_average_by_season)+sum(sum_daily_battery_contribution))/sum(pjm_daily_total_by_season),2))
Estimate Solar + Storage Market Share
2021 July 22 Twitter Substack See all postsA Python script that parses data and calculates solar + storage economics.
The summary of the process is:
Use NREL PV Watts modeling to obtain hourly power estimates.
Compare the hourly estimates to seasonal PJM demand data.
Obtain historical, hourly pricing data for PJM.
Determine how much demand not being met by panels is cost-effective to be arbitraged by batteries with the extra DC production
There are many assumptions and simplifications. I'd be happy if this had one sig fig accuracy. The one that bothers me the most is that when you create an average day and match it to peak demand, the average includes some days that might produce more than demand. In real life, electricity demand constrains output. Batteries and higher DC to AC ratios make this less relevant. So the cases with no storage and especially the lowest DC to AC ratios are probably overstated.
PV Watts
NREL PV Watts Calculator
These are the settings I put in the PV Watts model. Charlottesville is a random location within PJM. I titled the array slightly more than max power production so that the ratio of summer to winter power production would be more favorable. The calculator offers an option to download the hourly data as a CSV file.
PJM Comparison
I'll walk through the code step by step then put the entire script at the bottom.
First, we import the PV Watts CSV data:
I interpolated the PJM data from this chart:
Source: PJM Learning Center
The structure is [[winter hours 0-23], [spring hours 0-23], [summer hours 0-23], [fall hours 0-23]] with the index in the nested arrays being the hour.
And the sum of the average day for each season, using Riemann Sums:
We need a data structure that allows the grouping of all data points for an hour and season. This function generates a data structure similar to our PJM data.
And we need a data structure for averaged values, the same as the PJM daily total data structure.
We have to sort and average all the hourly data to create an "average day" to match our PJM average days for each season.
The way the PV Watts outputs the data makes it challenging to compare DC to AC ratios the way I wanted to. We will use one case and manually size the system using ratios and calculate our own AC outputs from DC values.
Now, let's average all our data points to create an average day for each season.
Our averages are for a 1 kW AC system. The system size is adjusted to meet 100% of the noon summer demand, using the 1:1 DC to AC ratio. The tilt we set for our panels means peak production doesn't always happen in summer, and the inverter is not 100% utilized. Increasing DC to AC ratio uses more of the inverter and decreases our adjusted system size, which is not the comparison I wanted.
We can get the total energy usage for each day and see what solar contributed.
Battery Arbitrage
Now to add some batteries. We have extra DC power. But the batteries have to be profitable. We can download a historical section of electricity price data from PJM's website. PJM Data Miner. I used June 2020-June 2021. I was a little worried about pandemic effects, but I spot-checked the 2019 data, and the basic averages were pretty close.
And sort the data by season:
Then sort by the hour. The PJM data is not as friendly to our data structure, so there is a dictionary to put the data in the correct hour.
Now we can create our hourly price averages for an average day in each season:
Ok, now we have solar data and price data. We will have to determine how much energy is available to arbitrage, how much demand there is, and specify our battery capacity. Here are a few things I might be glossing over:
High battery capacity to power requirements for 10+ hour storage means power was not considered a limitation.
This doesn't account for all the things batteries can do to earn money, including frequency regulation or multiple cycles per day. We are assuming a 24-hour cycle.
I left out battery efficiency. Depending on the solar farm and battery DC voltage, the efficiency will be 94%-97%.
We set up data structures for demand, extra DC electricity, and arbitrage prices.
Run through each hour to determine extra demand, what prices are, and what extra DC is available.
Now we have to sum our hours to get our daily demand:
Next, we need to approximate battery revenue per cycle. Batteries will arb the highest prices first, so we order the juiciest hours first.
And now we use a weighted average to see what the average price our batteries got was.
Now that we know revenue, we can guess the battery CAPEX needed to break even.
And we can do our final calculations:
Full code: